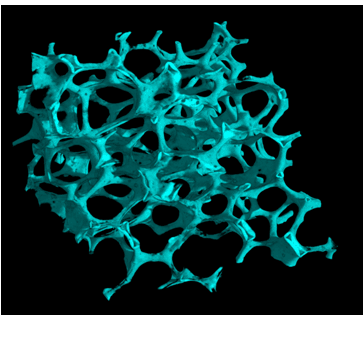
Tomography-Based Determination of Effective Heat/Mass Transport Properties for Complex Multi-Phase Media

Funding source: external page Swiss National Science Foundation 
Partner: external page Laboratory for Electronics/Metrology, EMPA Material Science and Technology, external page Swiss Light Source 

Objective – Development of a computer tomography based methodology for the determination of the effective heat/mass transport properties of complex porous materials. The focus is on porous materials applied in high-temperature solar thermal and thermochemical processes for producing power and fuels. The morphological characterization and accurate determination of the effective transport properties are crucial for the optimal design and efficient operation of solar receivers and reactors.

Background – Porous materials (e.g., reticulate porous ceramics, foams, porous monoliths, packed beds) are advantageous as heat exchangers and catalyst supports because of their unique combination of high specific surface area, high permeability, and high convection heat transfer coefficient. These materials can serve beneficially as radiant absorbers of concentrated solar energy and as components of solar receivers and reactors in high-temperature solar energy applications.

Approach – The exact 3D digital geometry of complex porous structures is obtained by computer tomography and used in direct pore-level simulations to numerically calculate their effective transport properties. Finite volume techniques are applied for conductive/convective heat transfer and fluid flow. Collision-based Monte Carlo method is applied for the radiative heat transfer. The effective transport properties determined are:

• morphological: porosity, pore size distribution, specific surface area, representative elementary volume
• radiation heat transfer: extinction coefficient and scattering phase function
• conduction heat transfer: effective thermal conductivity
• convection heat transfer: heat transfer coefficient
• fluid flow across porous media: permeability, Forchheimer coefficient, residence time and tortuosity distributions, diffusion tensor

These effective transport properties can be used in volume-averaged (continuum) heat and mass transfer models, which in turn can be applied for the design and optimization of components for high-temperature applications.